初中三年级（上）数学诊断训练九
班级____________ 名字____________ 学号____________ 成绩____________
1．如图，在
正方形网格中，一条圆弧经过
，
，
三点，那样这条圆弧所在圆的圆心是（ ）
A．点
B．点
C．点
D．点
2．如图所示，
内接于
，若
，则
的大小是（ ）
A．
B．
C．
D．
3．如图，
是的直径，弦交于点
，且
，
，则的半径为（ ）
A．4 B．5 C．4 D．3
4．如图，，
，，则以下结论：①
是
的平分线；②
③
；④
；其中正确的有（ ）
A．4 B．3 C．3 D．1
5．下列语句中，正确的个数有（ ）
①在圆中，相等的圆心角所对的弧相等②平分弦的直径垂直于弦③长度相等的两条弧相等④圆是轴对称图形，任何一条直径都是它的对称轴⑤等弧所对的圆心角相等，所对的弦相等；⑥圆内两条非直径的相交弦不可以互相平分
A．2 B．3 C．4 D．5
6．如图是小明完成的，作法是：取的直径，在上任取一点引弦
，当点在半圆上移动时（点不与、重合），
的平分线与的交点必（ ）
A．平分弧 B．三等分弧
C．到点
和直径的距离相等 D．到点和点的距离相等
2、填空题：
7．一个点到圆的最大距离为，最小距离为
，则圆的半径为__________；
8．已知矩形
的边
，
，以点为圆心作圆，使，，三点至少有一点在
内，且至少有一点在外，则的半径
的取值范围是__________；
9．在中，
，
，
，以点为圆心，以
为半径作圆，则点和的地方关系是__________；
10．一条弦把圆分成两部分，则弦所对的圆心角为__________；
11．如图所示，为圆
的直径，是圆的弦，和的延长线交于点，已知
，
，
的度数为__________；
12．下列命题中：①相等的弦所对的圆心角相等；②相等的圆心角所对的弧未必相等；③半圆是中心对称图形；④最长的弦是直径，其中是真命题的序号为__________；
13．的半径为，弦，，
，则和的距离为__________；
14．为美化校园，学校决定将花园边墙上的矩形门改为以
为直径的圆弧形门，如图所示，量得矩形门宽为
，对角线的长为
，则要打掉的墙体面积为__________；（结果保留
和根号）
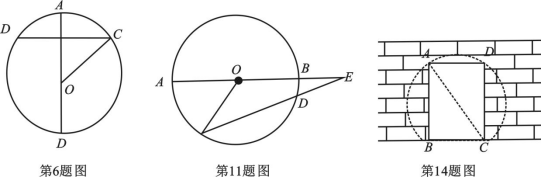
15．已知如图，为圆心，，弓形高，矩形
的两顶点，
在弦上，
，
在弦上，且，则
的长为__________；
16．如图
半径为1，圆心坐标为，点是内或上的一个动点，则
的最小值是__________；
17．如图，的半径弦于点，连结
并延长交于点，连结
，若，，则的长为__________；
18．如图，是的直径，，点在上，，为弧的中点，是直径上一动点，则的最小值为__________；
3、几何计算及证明：
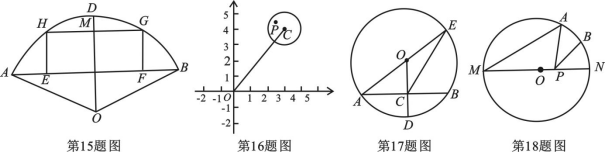
19．圆中弦、相交于，且，求证：
E
；
20．如图，已知弧上的三点，，．
（1）用尺规作图，画出
所在圆的圆心（保留作图痕迹，不写作法）；
（2）设边，，、的距离之差为，求圆片的半径．
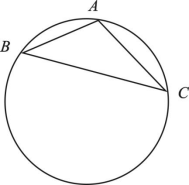
21．圆内接中，，圆心到的距离为，圆的半径为，求腰的长．
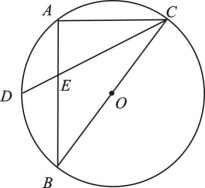
22．如图，
内接于，为直径，，，是的中点，与的交点为，求
的值．
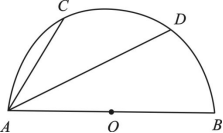
23．如图，半圆的直径，弦，平分，求的长．
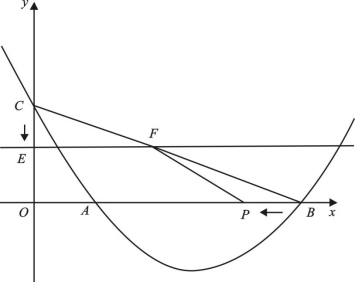
24．如图，抛物线交轴于、两点（点在点左边），交轴于点．已知，，的面积为8．
（1）求抛物线的分析式；
（2）若动直线（轴）从点开始，以每秒1个长度单位的速度沿轴负方向平移，且交轴、线段于、两点，动点同时从点出发，在线段
上以每秒2个单位的速度向原点运动．连接，设运动时间秒．当为什么值时，的值最大，求出最大值；
（3）在满足（2）的条件下，是不是存在的值，使以、、为顶点的三角形与相似．若存在，试求出的值：若没有，请说明理由．
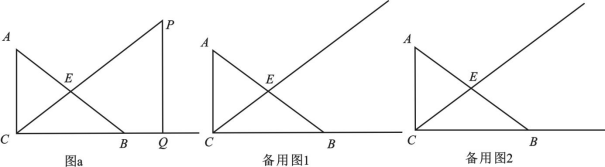
25．如图a，在中，，
是斜边上的中线，
，，点是延长线上的一动点，过点作，交延长线于点，设，．
（1）求关于的函数关系式及概念域；（4分）
（2）联结，当平分时，求
的长；（4分）
（3）过点作
交
于，当
和
相似时，求的值．（6分）
