21.1 整式方程 同步训练
1、选择题
1．把方程
中分母化整数，其结果应为（）
A．
B．0
C．
D．0
2．下列等式变形中，不正确的是．
A．看x＝y，则x+5＝y+5 B．若
，则x＝y
C．若-3x＝-3y，则x＝y D．若mx＝my，则x＝y
3.已知1是关于x的一元二次方程（m﹣1）x2+x+1=0的一个根，则m的值是（）
A.1 B.﹣1 C.0 D.没办法确定
4．若一元二次方程式ax（x＋1）＋（x＋1）（x＋2）＋bx（x＋2）＝2的两根为0．2，则|3a＋4b|之值为什么（）
A．2 B．5 C．7 D．8
5．某品牌服饰原价173元，连续两次降价
后价格价为127元，下面所列方程中正确的是（ ）
A．
B．
C．
D．
6．将代数式
化成的形式，正确的是（）
A. 
B. 
C. 
D. 
2、填空题
7．已知方程
的一个根为-1，则另一个根是______________________________，
的值是______________________________．
8.方程x（x﹣3）=3（3﹣x）的解是______________________________．
9．关于
的一元二次方程有一个根为0，则
__________.
10．问题1：设a、b是方程x2＋x－2012＝0的两个实数根，则a2＋2a＋b的值为__________；
问题2：方程x2－2x－1＝0的两个实数根分别为x1，x2，则（x1―1）（x2―1）＝__________；
某校2010年捐款1万元给期望工程，将来每年都捐款，计划到2012年共捐款4.75万元，则该校捐款的平均年增长率是__________.
3、解答卷
12.解下列关于x的方程
13. 解下列方程：
14.解方程
（1）2x2+3x+1=0
（2）（3x+1）2=9x+3．
15. 解下列方程：
参考答案
1．【答案】C；
【分析】解：依据分式的性质，每一个分式分子分母同乘以10得：．注意分式的基本性质与等式的性质的不同的地方．故选C．
2. 【答案】D
【分析】D中由mx＝my左右两边需同时除以m，得到x＝y，但当m＝0时，左右两边不可以同时除以m，所以D项中等式变形不正确，借助性质2对等式两边同时进行变形，特别注意等式两边同时除以一个式子时，肯定先确定这个式子不是0．
3.【答案】B；
【分析】解：依据题意得：（m﹣1）+1+1=0，
解得：m=﹣1．
故选B．
4.【答案】B；
【分析】先依据一元二次方程式ax（x＋1）＋（x＋1）（x＋2）＋bx（x＋2）＝2的根确定a．b的
关系式．然后依据a．b的关系式得出3a＋4b＝－5．用求绝对值的办法求出所需绝对值．
5.【答案】C；
【分析】当产品首次降价x%时，其价格为173－173x%＝173（1－x%）；
当产品第二次降价x%后，其价格为
173（1－x%）－173（1－x%）x%＝173（1－x%）2．
∴173（1－x%）2＝127．
故选C．
6.【答案】C；
【分析】．
7．【答案】3，-2．
【分析】设方程的另一个解是
，则
，解得．
8.【答案】x1=3，x2=﹣3；
【分析】解：原方程移项得，
x（x﹣3）+3（x﹣3）=0，
∴（x﹣3）（x+3）=0，
解得x1=3，x2=﹣3．
故答案为x1=3，x2=﹣3．
9．【答案】-1；
【分析】把x=0代入方程得
,由于，所以
.
10．【答案】2011；-2；
【分析】因为a，b是方程x2+x-2012=0的两个实数根，依据根与系数的关系可以得到a+b=-1，
并且a2+a-2012=0，然后把a2+2a+b可以变为a2+a+a+b，把前面的值代入即可求出结果．
11．【答案】50%；
【分析】
设该校捐款的平均年增长率是x，
则
，
整理，得
，
解得，
答：该校捐款的平均年增长率是50%.
12.【答案与分析】
（1）去括号，得 3ax-2x=6-2x
移项，得 3ax-2x+2x=6
合并相同种类项，得 3ax=6 ※
当a≠0时，方程※是一元一次方程，解得 
；
当a=0时，方程※变成 0·x=6，这个时候不论x取什么值，等式0·x=6都不成立，因此方程无解。
所以，当a≠0时，原方程的根是；当a=0时，原方程无解。
（2）移项，得 bx2+x2=1+1
合并相同种类项，得（b+1）x2=2
由于b≠-1，所以b+1≠0
两边同除以b+1，得 ※
当b+1＞0时，由方程※解得 ；
当b+1＜0时，方程※中
，这个时候方程没实数根。
所以，当b+1＞0时，原方程的根是
，
；
当b+1＜0时，原方程没实数根。
13.【答案与分析】（1）方程左侧因式分解，得
x=0
x=0
得x=0或x+4=0或2x-1=0
∴原方程的根是 x=0，x=-4，x=
注意：不要漏掉x=0这个根!
（2）方程左侧因式分解，得
+=0
x2+=0
（x-2）=0
即 x-2=0或x2+1=0
解方程x-2=0得 x=2
方程x2+1=0没实数根
所以，原方程的根是 x=2
14.【答案与分析】
解：（1）分解因式得：（2x+1）（x+1）=0，
可得2x+1=0或x+1=0，
解得：x1=﹣0.5，x2=﹣1；
（2）方程整理得：（3x+1）2﹣3（3x+1）=0，
分解因式得：（3x+1）（3x+1﹣3）=0，
可得3x+1=0或3x﹣2=0，
解得：x1=﹣
，x2=．
15.【答案与分析】察看方程的系数，可以发现系数有以下特征：x4的系数与常数项相同，x3的系数与x的系数相同，像如此的方程大家称为倒数方程．由
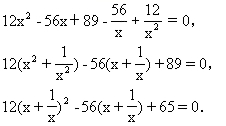
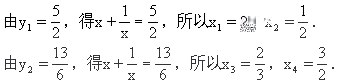
