7.5 画角的和、差、倍
班级__________ 名字__________ 学号__________
【学习计划/难题重点】
理解角平分线的定义,学会用量角器画角平分线的办法,体验类比的数学思想,初步领会角平分线的几何符号表示办法,感知几何符号语言的简洁性,会用尺规作出已知角的平分线,探究用尺规法作出45度、90度等特殊角的办法.
1、课前复习:
1.定义:__________叫做这条线段的中点.
2.如图,若已知点M是线段AB的中点,你能得到什么等量关系.![]()
![]()
![]()
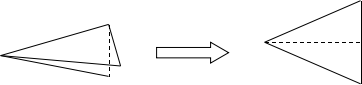 1.实验操作:用纸片作材料任意剪一个角,折叠这张纸片,使角的两边叠合在一块,再展开摊平.
1.实验操作:用纸片作材料任意剪一个角,折叠这张纸片,使角的两边叠合在一块,再展开摊平.
2.考虑:中间的折痕大家把它称作什么?假如把角的两边无限延伸,那样这条折痕是直线、线段还是射线?
定义——角平分线的概念:
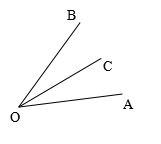 概念:__________叫做这个角的平分线.
概念:__________叫做这个角的平分线.
几何表示:假如OC是![]() 的平分线,那样也可以说成是OC平分
的平分线,那样也可以说成是OC平分![]() ,则有:
,则有:
 例题1:如图,
例题1:如图,![]() ,OB是
,OB是![]() 的平分线,那样
的平分线,那样![]() ,
,
![]() .
.
例题2.如图,已知![]() ,画出它的角平分线OC.
,画出它的角平分线OC.
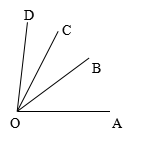
 例题3:如图,
例题3:如图,![]() ,
,![]()
1)用含m,n的式子分别表示![]() ,
,![]() 的度数,
的度数,
2)比较![]() ,
,![]() 的大小
的大小
考虑并操作:怎么样用尺规作出90度直角与45度角?
训练.如图,BD平分∠ABC,BE分∠ABC分2:5两部分,∠DBE=21°,求∠ABC的度数.
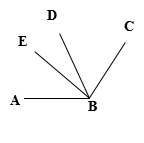
课课精炼
1、填空题:
 1.从一个角的__________点引出的一条__________线,把这个角分成两个__________的角,这条射线叫做这个角的__________.
1.从一个角的__________点引出的一条__________线,把这个角分成两个__________的角,这条射线叫做这个角的__________.
如图,由于 ![]() 平分
平分![]() ,
,
所以 ![]()
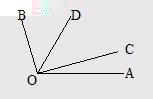 或
或![]()
2.如上图,![]() ,则
,则![]() 为
为![]() 的角平分线.
的角平分线.
3.如图,![]() ,
,
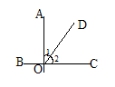
![]()
4. 如图,![]() 90°,
90°, ![]() ,则
,则![]()
![]()
2、选择题:
5.已知![]() ,其角平分线为
,其角平分线为![]() ,
,![]() ,其角平分线为
,其角平分线为![]() ,则
,则![]() 的大小为 ( )
的大小为 ( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
6.点![]() 在
在![]() 的内部,下面的等式中,能表示
的内部,下面的等式中,能表示![]() 是
是![]() 的平分线的有( )
的平分线的有( )
①![]() ②
②![]()
③![]() ④
④![]()
A.1个 B.2个 C.3个 D.4个
3、解答卷:
7.用两种不一样的办法画出下图中![]() 的平分线.
的平分线.
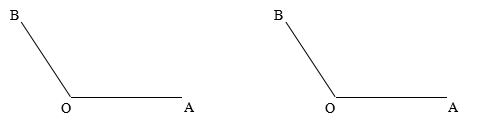
8.如图已知∠AOC=160 º,OD平分∠AOC,∠AOB是直角.求∠BOD的度数.
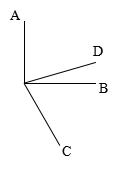
9.如图,OE平分![]() ,OD平分
,OD平分![]() ,
,![]() 求
求![]() 的度数.
的度数.
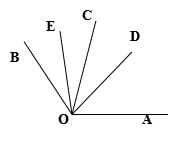
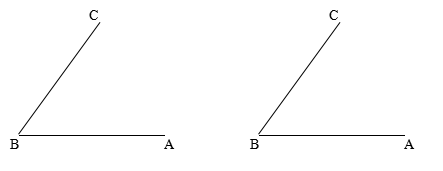
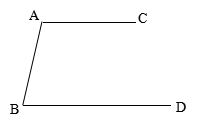
10. 操作与理解:如图,
1)分别作出∠A、∠B的平分线,并作出它们的交点O;
2)假如∠A的平分线与BD相交于E点,通过测量,判断△ABE的形状.
__________







