4.2 三角形的定义与性质（A--尝试训练）

学校____________________

班级____________________

名字____________________

（一）考试知识点 5.14 三角形的有关定义，画三角形的高、中线、角平分线（Ⅱ）

学习计划：（1）了解三角形的高、中线、角平分线的定义；（2）会画三角形的高、中线、角平分   线；（3）了解三角形的三条中线交于一点、三条角平分线交于一点、三条高所在直线交于一点及这   些交点的地方状况.

1．数学课上，小明进行了如下的尺规作图（如图所示）：

（2）分别以点 D、E为圆心，以大于DE为半径作弧，两弧交于△AOB内的一点 C；

（3）作射线 OC交 AB 边于点 P．

那样小明所求作的线段 O P  是△A O B 的 （ ）

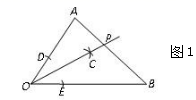A．一条中线； B．一条高； C．一条角平分线； D．不确定．

2．在图 2 中按需要尺规作图并完成填空：

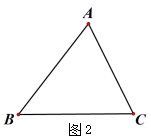（1）画出 BC 边的中线 AD；

（2）画出 BC 边的高，垂足为 E；

（3） ∵AD 是 BC 边的中线，

∴____________________=____________________.

∴ SDABD____________________SDACD

3. 已知 AD 、 BE 是△ ABC 的中线， AD 、 BE 相交于G 点， AD = 6 ，那样 AG =____________________.

4. 三角形三条高所在直线的交点在三角形的外部，那样这个三角形是 （ ）

A.直角三角形 B.锐角三角形 C.钝角三角形 D.没办法确定

5. 在△ ABC 中，AD、BE 分别是 BC 、 AC 上的中线，若 AB=20 米，那样 DE=____________________米.

（二）考试知识点 5.14 三角形的外角性质（Ⅱ）

学习计划：（1）了解三角形的外角的定义，并了解三角形的外角和等于   360°；（2）了解三角形外角的性质.

1. 三角形三个外角的度数之比是 2：3：4，则这个三角形三个内角的度数分别是____________________

2．已知等腰三角形的一个外角等于 110º，则该三角形的一个底角是（ ） A．35º B．70º或 110º C．70º D． 55º或 70º

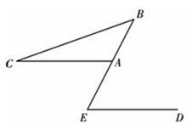
3. 如图 3， D 是 AB 上一点， E 是 AC 上一点， BE 、CD相交于点 F ，∠ A = 62°，

∠ ACD = 35°，∠ ABE = 20°.则∠ BDC =____________________， ÐBFC =____________________.

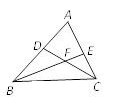图 3

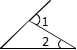
4.下列图形中，能确定Ð1肯定大于Ð2 的是（ ）

________________________________________

____________________

2

（A） （B） （C） （D）

5. 如图 4，已知 AC∥ED，∠C =26°，∠C B E =37°，则∠B E D  的度数是  A．63° B．83° C．73° D．53°

图 4

（三）考试知识点 5.15 三角形的任意两边之和大于第三边的性质（Ⅲ）

学习计划：（1）学会三角形的任意两边之和大于第三边的性质；（2）会运用三角形三边关系对三   角形的构成做出正确判断.

1.已知在△ABC 中，AB=3，BC=7，那样第三边 AC 长度的取值范围是____________________.

2. 在下列长度的三条线段中，不可以组成三角形的是（ ）

A．2cm，3cm，4cm B．3cm，6cm，76cm

C．2cm，2cm，6cm D．5cm，6cm，7cm

3. 已知△ABC 是等腰三角形，AB=2cm，AC=4cm,那样△ABC 的周长为____________________cm.

4. 菱形 ABCD 的一条对角线长为 6，边 AB 的长是方程的一个根，则菱形 ABCD 的周长为__________．

5. 已知 n 是正整数，若一个三角形的三条边长分别是 n + 2、 n + 8 、3n ，则满足条件的 n 的值有

A． 4 个 B．5 个 C．6 个 D．7 个

（四）考试知识点 5.15 三角形的内角和（Ⅲ）

学习计划：（1) 学会三角形的内角和等于 180°.（2）能运用三角形的内角性质进行简单的说理计算，初步历程和体验几何推理的过程.

1. 已知在△A B C  中，∠A =25°，∠C -∠B=15°，那样∠C=____________________度.

2． 在△ ABC 中，已知∠ A ：∠ B ：∠C=1：3：5，那样∠ A 、∠ B 、∠ C 的度数分别为____________________.

3. 已知等腰三角形的一个内角等于 70°，则这个等腰三角形的顶角等于____________________度.

4. 如图 5，在 △ABC 中，AD 是高，AE、BF 是角角平分线相交于点 O，∠BAC=50°，∠C=70°， 则∠DAC=____________________，∠BO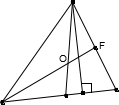A=____________________.

A

C

B E    D

图 5

5. 如图    6，已知在△A B C 中，∠BAC =70°，D 是边 BC 上一点，且∠CAD =∠C，

∠ADB = 80°. 求∠B、∠C的度数.

图 6

（五）考试知识点 5.19 命题、定理、证明、逆命题、逆定理的有关定义（Ⅱ）

学习计划：（1）了解基本的逻辑术语，并了解演绎推理的规则和规范表达；（2）了解命题、定理、   证明的意义（3）学会文字语言、图形语言和符号语言的表述及相互“转译”（4）了解逆命题与逆定理.

“对顶角相等”的逆命题是 __________，  这个命题是 __________命题.（填“真”或“假”）

下列命题中，真命题是（ ）

有一个角为锐角的三角形是锐角三角形 ；

不在同一直线的三条线段联结所组成的图形是三角形 ；

三角形按边分类可分为不等边三角形、等腰三角形和等边三角形；

三角形的一条中线把三角形分成面积相等的两部分.

下列定理中，具备逆定理的是（ ）

全等三角形的对应角相等；

菱形的对角线互相平分；

全等三角形的对应边相等；

正方形的对角线互相垂直 .

命题“假如三角形的一个外角平分线平行于这个三角形的一条边，那样这个三角形中的两个角相   等”是不是正确？并说明理由.